SENO, COSSENO E TANGENTE

Seno, Cosseno e Tangente de um ângulo são relações entre os lados de um triângulos retângulos. Essas relações são chamadas de razões trigonométricas, pois resultam da divisão entre as medidas dos seus lados.

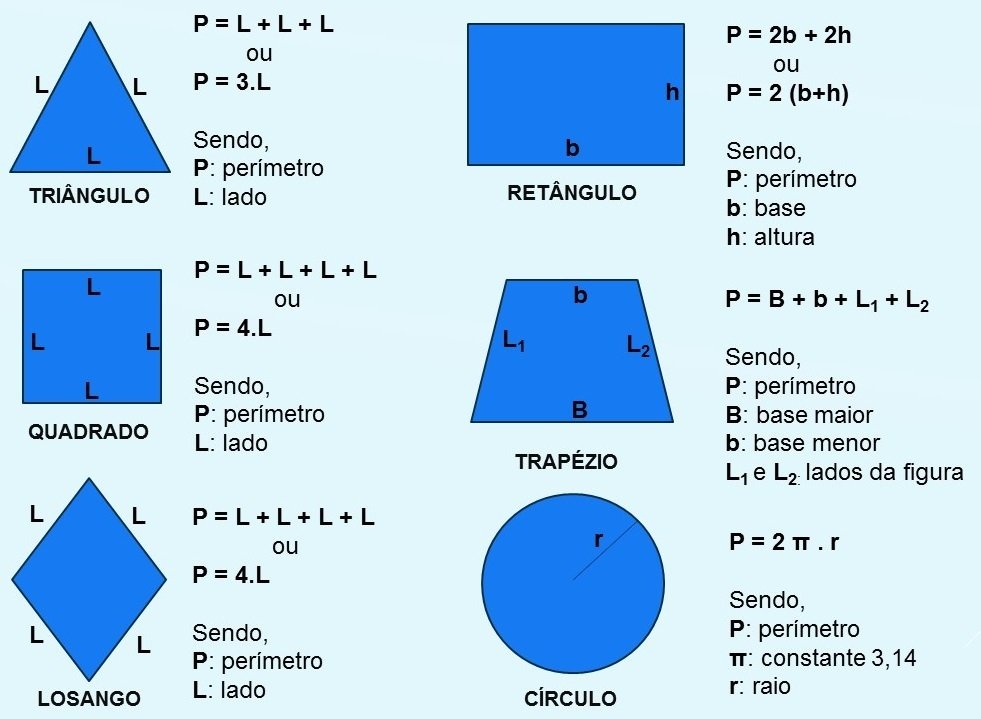
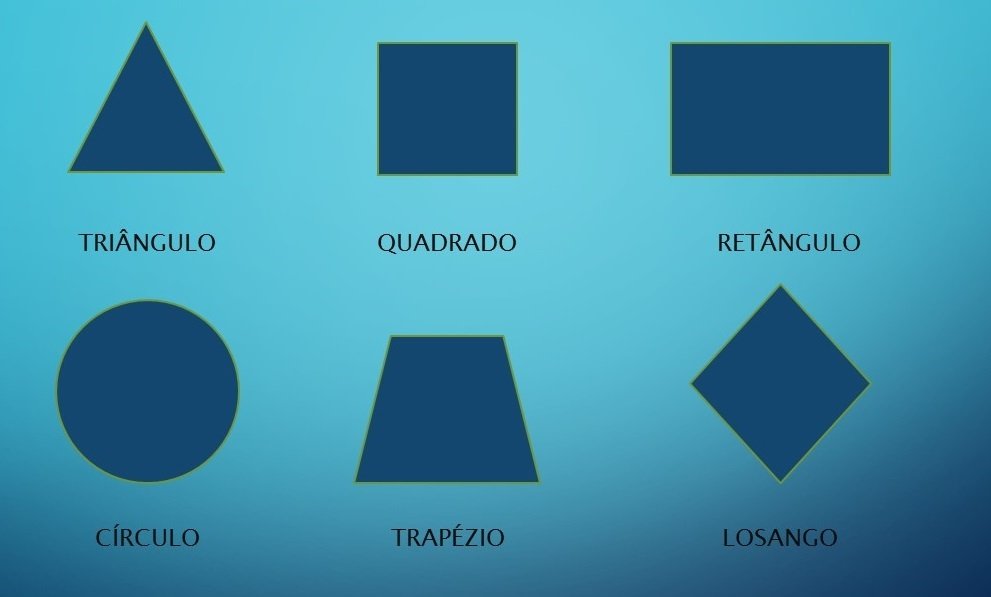
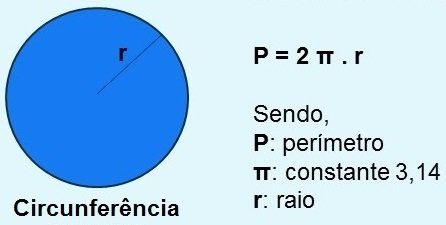
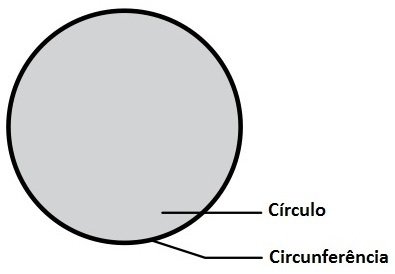
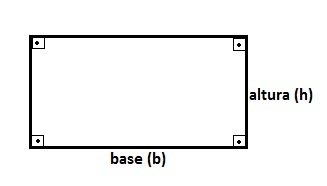
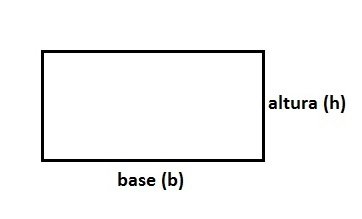
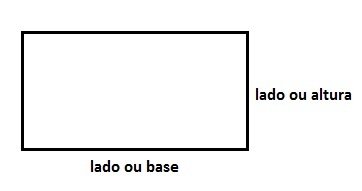
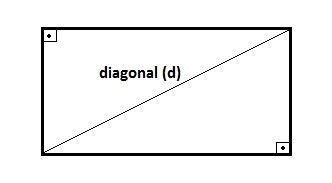
O triângulo retângulo é aquele que apresenta um ângulo interno reto (igual a 90º). O lado oposto ao ângulo de 90º é chamado de hipotenusa e os outros dois lados são chamados de catetos.

Os valores do seno, do cosseno e da tangente são calculados em relação a um determinado ângulo agudo do triângulo retângulo.


De acordo com a posição dos catetos em relação ao ângulo, ele pode ser oposto ou adjacente, conforme imagem abaixo:

Seno (Sen  )

É a razão entre a medida do cateto oposto ao ângulo agudo e a medida da hipotenusa de um triângulo retângulo. Essa relação é calculada através da fórmula:

Cosseno (Cos )

É a razão entre a medida do cateto adjacente ao ângulo agudo e a medida da hipotenusa de um triângulo retângulo. Essa relação é calculada através da fórmula:

Tangente (Tg )

É a razão entre a medida do cateto oposto e a medida do cateto adjacente ao ângulo agudo de um triângulo retângulo. Essa relação é calculada através da fórmula:

Tabela Trigonométrica

Na tabela trigonométrica consta o valor de cada razão trigonométrica para os ângulos de 1º a 90º.

Os ângulos de 30º, 45º e 60º são os mais usados nos cálculos e por isso, eles são chamados de ângulos notáveis.

TEORIA EUCLIDIANA

Alguns conceitos importantes da geometria euclidiana nos estudos da trigonometria são:

Lei dos Senos

A Lei dos Senos estabelece que num determinado triângulo, a razão entre o valor de um lado e o seno de seu ângulo oposto, será sempre constante.


Dessa forma, para um triângulo ABC de lados a, b, c, a Lei dos Senos é representada pela seguinte fórmula:




Lei dos Cossenos

A Lei dos Cossenos estabelece que em qualquer triângulo, o quadrado de um dos lados, corresponde à soma dos quadrados dos outros dois lados, menos o dobro do produto desses dois lados pelo cosseno do ângulo entre eles.

Dessa maneira, sua fórmula é representada da seguinte maneira:




Lei das Tangentes

A Lei das Tangentes estabelece a relação entre as tangentes de dois ângulos de um triângulo e os comprimentos de seus lados opostos.

Dessa forma, para um triângulo ABC, de lados a, b, c, e ângulos α, β e γ, opostos a estes três lados, têm-se a expressão:





Teorema de Pitágoras

O Teorema de Pitágoras, criado pelo filósofo e matemático grego, Pitágoras de Samos, (570 a.C. - 495 a.C.), é muito utilizado nos estudos trigonométricos.

Ele prova que no triângulo retângulo, composto por um ângulo interno de 90° (ângulo reto), a soma dos quadrados de seus catetos corresponde ao quadrado de sua hipotenusa:

a2 = c2+ b2

Sendo,

a: hipotenusa

c e b: catetos

TRIGONOMETRIA

A trigonometria é uma parte da matemática que as diferenças entre os lados e os ângulos dos triângulos.

Ela é aplicada também em outras áreas do estudo como física, química, biologia, geografia, astronomia, medicina, engenharia, etc.

RELAÇÕES TRIGONOMÉTRICAS DO TRIÂNGULO RETÂNGULO

As razões trigonométricas são as relações existentes entre os lados de um triângulo retângulo. As principais são o seno, o cosseno e a tangente.


Lê-se cateto oposto sobre a hipotenusa.



Lê-se cateto adjacente sobre a hipotenusa.



Lê-se cateto oposto sobre o cateto adjacente.



Círculo trigonométrico e as razões trigonométricas


O círculo trigonométrico é utilizado para auxiliar nas relações trigonométricas. Acima, podemos encontrar as principais razões, sendo que o eixo vertical corresponde ao seno e o eixo horizontal ao cosseno. Além delas, temos as razões inversas: secante, cossecante e cotangente.

TRIGONOMETRIA NO TRIÂNGULO RETÂNGULO

A trigonometria no triângulo retângulo é o estudo sobre os triângulos que possuem um ângulo interno de 90°, chamado de ângulo reto.

Lembre-se que a trigonometria é a ciência responsável pelas relações estabelecidas entre os triângulos. Eles são figuras geométricas planas compostas de três lados e três ângulos internos.

O triângulo chamado equilátero possui os lados com medidas iguais. O isósceles possui dois lados com medidas iguais. Já o escaleno tem os três lados com medidas diferentes.

No tocante aos ângulos dos triângulos, os ângulos internos maiores que 90° são chamados de obtusângulos. Já os ângulos internos menores que 90° são denominados de acutângulos.

Além disso, a soma dos ângulos internos de um triângulo será sempre 180°.



Composição do Triângulo Retângulo

O triângulo retângulo é formado:

Catetos: são os lados do triângulo que formam o ângulo reto. São classificados em: cateto adjacente e cateto oposto.

Hipotenusa: é o lado oposto ao ângulo reto, sendo considerado o maior lado do triângulo retângulo.


Segundo o Teorema de Pitágoras, a soma dos quadrado dos catetos de um triângulo retângulo é igual ao quadrado de sua hipotenusa:

h2 = ca2 + co2

PERÍMETRO DO CÍRCULO

O perímetro do círculo corresponde a medida da volta completa dessa figura geométrica plana. Nesse caso, o perímetro é o comprimento da circunferência.

Lembre-se se que o perímetro é a soma de todos os lados da figura. Por exemplo, se vamos encontrar o perímetro do triângulo, devemos somar o valor das medidas dos três lados da figura.

Fórmula do Perímetro

Vale lembrar que o círculo é uma figura que não apresenta segmentos de retas. Portanto, o perímetro do círculo equivale a soma total de seu contorno.

Assim, a fórmula é:

P = 2 π . r

Donde,

P: perímetro
π: constante de valor 3,14
r: raio

Fique Atento!
O valor do raio é determinante para encontrar o perímetro dessa figura. Assim, quanto maior o raio, maior será seu perímetro.

Feita essa observação, lembre-se que o raio é a medida do centro da figura até sua extremidade. Assim, o raio mede a metade do diâmetro.

ÁREA DO CÍRCULO

A área do círculo corresponde ao valor da superfície dessa figura, levando em conta a medida de seu raio (r).

O que é Círculo?

Vale lembrar que o círculo, também chamado de disco, é uma figura geométrica que faz parte dos estudos da geometria plana.

Essa figura surge na medida em que os polígonos regulares inscritos nela vão aumentando o número dos lados.



Ou seja, com o aumento do número de lados dos polígonos estes vão se aproximando da forma circular.

Fórmula: Cálculo da Área do Círculo
Para calcular a área do círculo devemos utilizar a seguinte fórmula:

A = π . r2

Onde,

π: constante Pi (3,14)
r: raio

Fique Atento!

Lembre-se que o raio (r) corresponde a distância entre o centro e a extremidade do círculo.



Já o diâmetro é um segmento de reta que passa pelo centro do círculo, dividindo-o em duas metades iguais. Dito isso, o diâmetro equivale duas vezes o raio (2r).

Perímetro do Círculo

O perímetro é um conceito da matemática que mede o comprimento (contorno) de determinada figura. Em outras palavras, o perímetro é a soma de todos os lados de uma figura geométrica.

No caso do círculo, o perímetro é chamado de circunferência e é calculado pelo dobro da medida do raio (2r). Assim, o perímetro da circunferência é medido pela fórmula:


P = 2 π . r



Diferença entre Círculo e Circunferência

Embora a maioria das pessoas acreditem que o círculo e a circunferência são as mesmas figuras, elas possuem diferenças.


Enquanto a circunferência é a linha curva que limita o círculo, o círculo é uma figura plana limitada pela circunferência.

ÁREA DO TRIÂNGULO

A área do triângulo pode ser calculada através das medidas da base e da altura da figura. Lembre-se que o triângulo é uma figura geométrica plana formada por três lados.

Contudo, há diversas maneiras de calcular a área de um triângulo, sendo que a escolha é feita de acordo com os dados conhecidos no problema.

Acontece que muitas vezes, não temos todas as medidas necessárias para fazer esse cálculo.

Nestes casos, devemos identificar o tipo de triângulo (retângulo, equilátero, isósceles ou escaleno) e levar em consideração as suas características e propriedades para encontrar as medidas que necessitamos.

Como calcular a área de um triângulo?


Na maioria das situações, usamos as medidas da base e da altura de um triângulo para calcular a sua área. Considere o triângulo representado abaixo, sua área será calculada, usando a seguinte fórmula:



Sendo,

Área: área do triângulo
b: base
h:altura

Área do Triângulo Retângulo

O triângulo retângulo possui um ângulo reto (90º), e dois ângulos agudos (menores que 90º). Desta maneira, das três alturas de um triângulo retângulo, duas coincidem com os lados desse triângulo.

Além disso, se conhecermos dois lados de um triângulo retângulo, usando o teorema de Pitágoras, facilmente encontramos o terceiro lado.




Área do Triângulo Equilátero

O triângulo equilátero, também chamado de equiângulo, é um tipo de triângulo que possui todos os lados e ângulos internos congruentes (mesma medida).

Neste tipo de triângulo, quando conhecemos apenas a medida do lado, podemos usar o teorema de Pitágoras para encontrar a medida da altura.

A altura, neste caso, o divide em outros dois triângulos congruentes. Considerando um desses triângulos e que seus lados são L, h (altura) e L/2 (o lado relativo a altura fica dividido ao meio), ficamos com:



Assim, substituindo o valor encontrado para a altura na fórmula da área, temos:



Área do Triângulo Isósceles

O triângulo isósceles é um tipo de triângulo que possui dois lados e dois ângulos internos congruentes. Para calcular a área do triângulo isósceles, utiliza-se a fórmula básica para um triângulo qualquer.
Quando queremos calcular a área de um triângulo isósceles e não conhecemos a medida da altura, também podemos usar o teorema de Pitágoras para encontrar essa medida.

No triângulo isósceles, a altura relativa a base (lado com medida diferente dos outros dois lados) divide este lado em dois segmentos congruentes (mesma medida).

Desta forma, conhecendo as medidas dos lados de um triângulo isósceles, podemos encontrar sua área.

Exemplo


Calcule a área do triângulo isósceles representado na figura abaixo:



Solução

Para calcular a área do triângulo usando a fórmula básica, precisamos conhecer a medida da altura. Considerando a base como o lado de diferente medida, iremos calcular a altura relativa a esse lado.

Lembrando que a altura, neste caso, divide o lado em duas partes iguais, usaremos o teorema de Pitágoras para calcular sua medida.




Área do Triângulo Escaleno

O triângulo escaleno é um tipo de triângulo que possui todos os lados e ângulos internos diferentes. Sendo assim, uma forma de encontrar a área desse tipo de triângulo é usar a trigonometria.

Se conhecermos dois lados desse triângulo e o ângulo entre esses dois lados, sua área será dada por:

   


Pela Fórmula de Heron também podemos calcular a área do triângulo escaleno.

Outras fórmulas para calcular a área do triângulo

Além da encontrar a área através do produto da base pela altura e dividir por 2, podemos também utilizar outros processos.

Fórmula de Heron

Outra maneira de calcular a área do triângulo é pela "Fórmula de Heron", também chamada de "Teorema de Herão". Ela utiliza os semiperímetros (metade do perímetro) e os lados do triângulo.



Onde,

S: área do triângulo
p: semiperímetro
a, b e c: lados do triângulo
Sendo o perímetro do triângulo a soma de todos os lados da figura, o semiperímetro representa a metade do perímetro:



Interessante notar que, nesta fórmula não há a necessidade de se conhecer a medida da altura (h), por isso, quando essa informação não é dada, o "Teorema de Heron" facilita encontrar a área do triângulo.

ÁREA DO LOSANGO

O Losango é uma figura geométrica plana representada por um quadrilátero equilátero, ou seja, um polígono formado por quatro lados iguais.

Importante destacar que todo losango é um paralelogramo, cujos lados opostos são iguais e paralelos, com duas diagonais que se cruzam perpendicularmente.

Diferente do quadrado, que possui quatro ângulos iguais a 90º, o losango possui dois ângulos agudos (menores que 90º) e dois ângulos obtusos (maiores que 90º).
Assim, enquanto o losango é um paralelogramo composto de quatro lados congruentes, o retângulo é um paralelogramo composto de quatro ângulos congruentes. Já o quadrado é um paralelogramo composto de quatro lados e quatro ângulos congruentes.

Fórmula da Área

Para calcular a área do losango é necessário traçar duas diagonais. Dessa forma tem-se 4 triângulos retângulos (com ângulo reto de 90º) iguais.

Assim, podemos encontrar a área do losango a partir da área de 4 triângulos retângulos ou 2 retângulos.

Assim, a fórmula para encontrar a área do losango é representada da seguinte maneira:



Sendo A, a área do losango, D1 a diagonal maior e D2 a diagonal maior.

ÁREA DO RETÂNGULO

A área do retângulo corresponde ao produto da medida da base pela altura da figura, sendo expressa pela fórmula:

A=b.h

Onde,

A: área
b: base
h: altura



Lembre-se que o retângulo é uma figura geométrica plana formada por quatro lados (quadrilátero). Dois lados do retângulo são menores e dois deles são maiores.

Ele possui quatro ângulos internos de 90° chamados de ângulos retos. Assim, a soma dos ângulos internos dos retângulos totalizam 360°.

PERÍMETRO E ÁREA DE FIGURAS PLANAS

É comum haver confusão entre o conceito de área e perímetro. No entanto, a área é a medida da superfície de uma figura plana. Já o perímetro é soma das medidas dos lados da figura.

Fórmulas dos Perímetros

Para calcular cada uma das figuras planas apresentadas acima, utilizam-se as seguintes fórmulas:

PERÍMETROS DE FIGURAS PLANAS

Os perímetros de figuras planas indicam o valor da medida do contorno da figura. Ou seja, o conceito de perímetro corresponde à soma de todos os lados de uma figura geométrica plana.

Vejamos abaixo as principais figuras que fazem parte da Geometria Plana.

Principais Figuras Planas

Triângulo: figura plana formada por três lados e ângulos internos. De acordo com a medida dos lados eles podem ser:

• Triângulo Equilátero: lados e ângulos internos iguais (60°);
• Triângulo Isósceles: dois lados e dois ângulos internos congruentes;
• Triângulo Escaleno: todos os lados e ângulos internos são diferentes.

E, de acordo com a medida dos ângulos, eles são classificados em:

• Triângulo Retângulo: um ângulo interno de 90°;
• Triângulo Obtusângulo: dois ângulos agudos internos (menor que 90°), e um ângulo obtuso interno (maior que 90°);
• Triângulo Acutângulo: três ângulos internos menores que 90°.

Quadrado: figura plana formada por quatro lados congruentes (mesma medida). Possui quatro ângulos internos de 90° (ângulos retos).

Retângulo: figura plana formada por quatro lados, donde dois deles são menores. Também possui quatro ângulos internos de 90°.

Círculo: figura plana que também é chamada de disco. É formado pelo raio (distância entre o centro e a extremidade da figura) e o diâmetro (segmento de reta que passa pelo centro e vai de um lado ao outro da figura.

Trapézio: figura plana formada por quatro lados. Apresenta dois lados e bases paralelas, sendo uma menor e outra maior. De acordo com a medida dos lados e ângulos eles são classificados em:

• Trapézio Retângulo: possui dois ângulos de 90º;
• Trapézio Isósceles ou Simétrico: os lados não paralelos possuem a mesma medida;
• Trapézio Escaleno: todos os lados possuem medidas diferentes.

Losango: figura plana formada por quatro lados iguais. Possui lados e ângulos opostos congruentes e paralelos.

CIRCUNFERÊNCIA

Circunferência é uma figura geométrica com formato circular que faz parte dos estudos de geometria analítica. Note que todos os pontos de uma circunferência são equidistantes de seu raio (r).

Raio e Diâmetro da Circunferência

Lembre-se que o raio da circunferência é um segmento que liga o centro da figura a qualquer ponto localizado em sua extremidade.

Já o diâmetro da circunferência é um segmento de reta que passa pelo centro da figura, dividindo-a em duas metades iguais. Por isso, o diâmetro equivale duas vezes o raio (2r).

Equação Reduzida da Circunferência

A equação reduzida da circunferência é utilizada para determinar os diversos pontos de uma circunferência, auxiliando assim, em sua construção. Ela é representada pela seguinte expressão:

(x - a)2 + (y - b)2 = r2

Onde as coordenadas de A são os pontos (x,y) e de C são os pontos (a,b).

Equação Geral da Circunferência

A equação geral da circunferência é dada a partir do desenvolvimento da equação reduzida.

x2 + y2 – 2 ax – 2by + a2 + b2 – r2 = 0

Área da Circunferência

A área de uma figura determina o tamanho da superfície dessa figura. No caso da circunferência, a fórmula da área é:

Perímetro da Circunferência

O perímetro de uma figura plana corresponde a soma de todos os lados dessa uma figura.

No caso da circunferência, o perímetro é o tamanho da medida do contorno da figura, sendo representado pela expressão:

Complemente seus conhecimentos com a leitura do artigo: Perímetros de Figuras Planas.

Comprimento da Circunferência

O comprimento da circunferência está intimamente relacionado com seu perímetro. Assim, quando maior o raio dessa figura, maior será seu comprimento.

Para calcular o comprimento de uma circunferência utilizamos a mesma fórmula do perímetro:

C = 2 π . r

Donde,

C: comprimento
π: constante Pi (3,14)
r: raio

Circunferência e Círculo

Muito comum haver confusão entre a circunferência e o círculo. Embora utilizamos esses termos como sinônimos, eles apresentam diferença.

Enquanto a circunferência representa a linha curva que limita o círculo (ou disco), este é uma figura limitada pela circunferência, ou seja, representa sua área interna.

RETÂNGULO

O retângulo é uma figura geométrica plana formada por quatro lados (quadrilátero). Dentre os lados, dois deles são menores, o que os difere dos quadrados.

Assim o retângulo é um paralelogramo formado por ângulos internos retos (90°) e congruentes (mesma medida).

Área do Retângulo

Para encontrar a área da superfície de um retângulo, basta multiplicar o valor da base pelo da altura.

Assim, a fórmula da área do retângulo é expressa da seguinte forma:

A=b.h

Donde,

A: área
b: base
h: altura

Perímetro do Retângulo

Já o conceito de perímetro é determinado pela soma de todos os lados da figura. No caso do retângulo corresponde a soma de duas vezes o valor da base e da altura.

É expresso pela fórmula:

P = 2(b + h)

Diagonal do Retângulo

Quando traçamos uma diagonal no retângulo, ele formará dois triângulos retângulos. Assim, para calcular a diagonal do retângulo utilizamos o Teorema de Pitágoras: a2=b2+c2.

Note que a diagonal corresponde a hipotenusa do triângulo retângulo. Logo, a fórmula da diagonal do retângulo é expressa da seguinte forma:

d2= b2 +h2ou d=√b2+h2

Donde,

d: diagonal
b: base
h: altura

Fique Atento!

Quando calculamos a área ou perímetro devemos levar em conta as unidades de medida. Ou seja, os valores devem estar na mesma unidade: centímetros, centímetros quadrados, metros, metro quadrados, etc.

Triângulo Retângulo

O triângulo é uma figura geométrica plana formada por três lados. O triângulo retânguloé uma figura que também faz parte da geometria plana. Recebe esse nome pois apresenta um ângulo reto, ou seja, de 90°.

Trapézio Retângulo

O trapézio é uma figura geométrica plana que possui dois lados e bases paralelas, donde uma é maior e outra menor.

Da mesma forma que os triângulos retângulos, o chamado trapézio retângulo recebe esse nome pois possui dois ângulos retos de 90º.

Retângulo Áureo

O retângulo áureo ou retângulo de ouro é um conceito da geometria euclidiana, o qual é também aplicado no campo das artes.

Trata-se de um caso de retângulo em que ao dividir a base pela sua altura, obtêm-se o valor de 1,618. Esse número é chamado de número de ouro.