COMO FAZER O CÍRCULO TRIGONOMÉTRICO ?

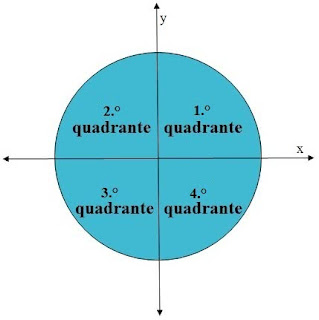
Para fazer um círculo trigonométrico, devemos construí-lo sobre o eixo de coordenadas cartesianas com centro em O. Ele apresenta um raio unitário e os quatro quadrantes.

CÍRCULO TRIGONOMÉTRICO E SEUS SINAIS

De acordo com o quadrante em que está inserido, os valores do seno, cosseno e tangente Varia.

Ou seja, os adultos podem apresentar um valor positivo ou negativo.

Para ver melhor, veja a figura abaixo:

QUADRANTES DO CÍRCULO TRIGONOMÉTRICO

Quando os indicadores trigonométricos e mensais são comparáveis, temos os quatro quadrantes que constituem. Para compreender melhor, observe a figura abaixo:

1. ° Quadrante: 0º
2. ° Quadrante: 90º
3. ° Quadrante: 180º
4. ° Quadrante: 270º

RADIANOS DO CÍRCULO TRIGONOMÉTRICO

A medida de um arco no círculo trigonométrico pode ser dada em grau (°) ou radiano (rad).

1 ° corresponde a 1/360 da circunferência. A circunferência é dividida em 360 partes ao longo do centro, sendo que cada uma tem uma razão que corresponde a 1 °.
1 radial corresponde à medida do arco da circunferência, cujo comprimento é igual ao raio da circunferência do arco que será medido.

Figura do Círculo Trigonométrico dos ângulos expressos em graus e radianos

Para auxiliar nas medidas, confira as diferenças entre graus e radianos:

π rad = 180 °
2π rad = 360 °
π / 2 rad = 90 °
π / 3 rad = 60 °
π / 4 rad = 45 °
Obs: Se quiser converter em unidades de medida (grau e radiano) use-se a regra de three.

Exemplo: Qual é a medida de um ângulo de 30 ° em radianos?

π rad -180 °
x - 30 °
x = 30 °. π rad / 180 °

x = π / 6 rad

ÂNGULOS NOTÁVEIS

Nenhum risco pode representar as razões trigonométricas de um qualquer ângulo da circunferência.

Chamamos de? Notáveis os mais conhecidos (30 °, 45 ° e 60 °). As razões trigonométricas são importantes são seno, cosseno e tangente:

CÍRCULO TRIGONOMÉTRICO

O Trigonométrico Círculo, também chamado de Ciclo ou Circunferência Trigonométrica, é uma representação gráfica que auxilia no cálculo das razões trigonométricas.
  
  Círculo trigonométrico e as razões trigonométricas

De acordo com uma simetria do círculo trigonométrico, o eixo vertical corresponde ao eixo e ao eixo horizontal ao cosseno. Cada ponto dele está associado aos valores dos ângulos.