COMO FAZER O CÍRCULO TRIGONOMÉTRICO ?

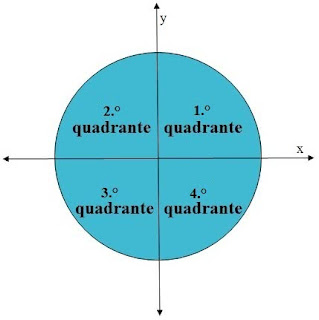
Para fazer um círculo trigonométrico, devemos construí-lo sobre o eixo de coordenadas cartesianas com centro em O. Ele apresenta um raio unitário e os quatro quadrantes.

CÍRCULO TRIGONOMÉTRICO E SEUS SINAIS

De acordo com o quadrante em que está inserido, os valores do seno, cosseno e tangente Varia.

Ou seja, os adultos podem apresentar um valor positivo ou negativo.

Para ver melhor, veja a figura abaixo:

QUADRANTES DO CÍRCULO TRIGONOMÉTRICO

Quando os indicadores trigonométricos e mensais são comparáveis, temos os quatro quadrantes que constituem. Para compreender melhor, observe a figura abaixo:

1. ° Quadrante: 0º
2. ° Quadrante: 90º
3. ° Quadrante: 180º
4. ° Quadrante: 270º

RADIANOS DO CÍRCULO TRIGONOMÉTRICO

A medida de um arco no círculo trigonométrico pode ser dada em grau (°) ou radiano (rad).

1 ° corresponde a 1/360 da circunferência. A circunferência é dividida em 360 partes ao longo do centro, sendo que cada uma tem uma razão que corresponde a 1 °.
1 radial corresponde à medida do arco da circunferência, cujo comprimento é igual ao raio da circunferência do arco que será medido.

Figura do Círculo Trigonométrico dos ângulos expressos em graus e radianos

Para auxiliar nas medidas, confira as diferenças entre graus e radianos:

π rad = 180 °
2π rad = 360 °
π / 2 rad = 90 °
π / 3 rad = 60 °
π / 4 rad = 45 °
Obs: Se quiser converter em unidades de medida (grau e radiano) use-se a regra de three.

Exemplo: Qual é a medida de um ângulo de 30 ° em radianos?

π rad -180 °
x - 30 °
x = 30 °. π rad / 180 °

x = π / 6 rad

ÂNGULOS NOTÁVEIS

Nenhum risco pode representar as razões trigonométricas de um qualquer ângulo da circunferência.

Chamamos de? Notáveis os mais conhecidos (30 °, 45 ° e 60 °). As razões trigonométricas são importantes são seno, cosseno e tangente:

CÍRCULO TRIGONOMÉTRICO

O Trigonométrico Círculo, também chamado de Ciclo ou Circunferência Trigonométrica, é uma representação gráfica que auxilia no cálculo das razões trigonométricas.
  
  Círculo trigonométrico e as razões trigonométricas

De acordo com uma simetria do círculo trigonométrico, o eixo vertical corresponde ao eixo e ao eixo horizontal ao cosseno. Cada ponto dele está associado aos valores dos ângulos.

UNIDADE DE MEDIDA

As unidades de medida são modelos para medir diferentes grandezas, tais como comprimento, capacidade, massa, tempo e volume.

O Sistema Internacional de Unidades (SI) define uma unidade padrão de cada grandeza. Based on system métrico decimal, o ID from the main use of immemorizing the unit of the countries.

Medidas de Comprimento

Há várias medidas de comprimento, como por exemplo uma jarda, uma polegada e o pé.

No SI a unidade é padrão de metro (m). O tempo é calculado como um intervalo de tempo percorrido pela luz durante um intervalo de tempo de 1 / 299.792.458 de segundo.

Os múltiplos e submúltiplos do metrô são: quilômetro (km), hectômetro (hm), decâmetro (barragem), decímetro (dm), centímetro (cm) e milímetro (mm).

Medidas de Capacidade

A unidade de medida de capacidade mais utilizada é o litro (l). São ainda usados o galão, o barril, o quarto, entre outras.

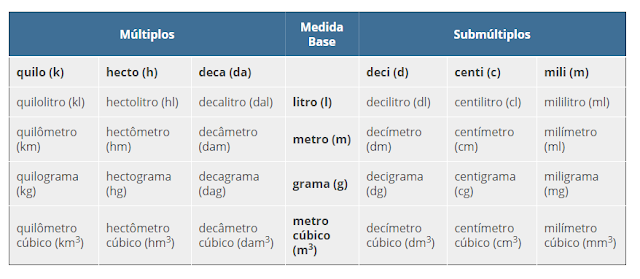
Os múltiplos e submúltiplos são: quilolitro (kl), hectolitro (hl), decalitro (dal), decilitro (dl), centilitro (cl), mililitro (ml).

Medidas de Massa

No Sistema Internacional de unidades de massa é o quilograma (kg). Um cilindro de platina e irídio é usado como o padrão universal do quilograma.

Como unidades de massa são: quilograma, hectograma, decagrama, grama, decigrama, centigrama e miligrama.

São ainda exemplos de medidas de massa de arroba, uma libra, uma onça e uma tonelada. Sendo 1 tonelada equivalente a 1000 kg.

Medidas de Volume

Não há unidade de volume no metrô cúbico (m3). Os múltiplos e submúltiplos são: quilômetro cúbico (km3), hectômetro cúbico (hm3), decâmetro cúbico (barragem3), decímetro cúbico (dm3), centímetro cúbico (cm3) e milímetro cúbico (mm3).

"Podemos transformar uma medida de capacidade em volume, pois os líquidos são uma forma de conter o que contém. Para isso usamos a seguinte relação:

1 l = 1 dm３

Tabela de conversão de Medidas

O mesmo método pode ser usado para calcular várias grandezas.

Primeiro, vamos desenhar uma tabela e colocar seu centro como unidades de base das grandezas que querem converter, por exemplo:

Capacidade: litro (l)

Comprimento: metro (m)

Massa: grama (g)

Volume: metro cúbico (m3)

Tudo o que é necessário para o mesmo direito da base são chamados submúltiplos. The prefixos deci, centi and mili prefixing for décima, centésima and milésima part of the unit fundamental.

Do lado esquerdo estão os múltiplos. Os prefixos deca, hectosem e quilo to correspondentemente, cem e mil vezes a unidade fundamental.

INTERVALOS NUMÉRICOS

Há um subconjunto relacionado com os números reais que são chamados de intervalos. Sejam os reais e os reais:

Intervalo aberto de extremos:] a, b [= {x ∈ R│a}

Intervalo fechado de extremos: [a, b] = {x ∈ R│a ≤ x ≤ b}

Intervalo aberto à direta (ou fechado à esquerda) de extremos: [a, b [= {x ∈ R│a ≤ x}



Intervalo aberto à esquerda (ou fechado à direita) de extremos:] a, b] = {x ∈ R│a}



Propriedades dos Conjuntos Numéricos




Para obter mais informações sobre os conjuntos de dados, siga abaixo algumas das suas propriedades:

O conjunto dos dados naturais (N) é um subconjunto dos números inteiros: Z (N ⊂ Z).

O conjunto dos números inteiros (Z) é um subconjunto dos números racionais: (Z ⊂ Q).

O grupo dos números racionais (Q) é um subconjunto dos números reais (R).

Os conjuntos de espécies naturais (N), inteiros (Z), racionais (Q) e irracionais (I) são subconjuntos dos números reais (R).

CONJUNTOS NUMÉRICOS

Os conjuntos numéricos reúnem são utilizados com elementos são números. Elas são formadas pelas naturais, inteiros, racionais, irracionais e reais.

Confira abaixo as características de cada conceito de símbolo, símbolo e subconjuntos.

Conjunto dos Números Naturais (N)
O agrupamento de unidades é representado por N. Ele reúne os números que usam para contar (incluindo o zero) e é infinito.

Subconjuntos dos Números Naturais

N * = {1, 2, 3, 4, 5 ..., n, ...} ou N * = N - {0}: conjuntos de números naturais não-nulos, ou seja, sem o zero.

Np = {0, 2, 4, 6, 8 ..., 2n, ...}, em que n ∈ N: conjunto dos grupos naturais pares.

Ni = {1, 3, 5, 7, 9 ..., 2n + 1, ...}, em que n ∈ N: conjunto dos números naturais e constantes.

P = {2, 3, 5, 7, 11, 13, ...}: conjunto dos números naturais primos.


Conjunto dos Números Inteiros (Z)
O conjunto dos números inteiros é representado por Z. Reúne todos os elementos dos bancos naturais (N) e seus opostos. Assim, conclui-se que N é um subconjunto de Z (N ⊂ Z):

Subconjuntos dos Números Inteiros
Z * = {..., –4, –3, –2, –1, 1, 2, 3, 4, ...} ou Z * = Z - {0}: contém os números 
inteiros não-nulos, ou seja, sem o zero.

Z + = {0, 1, 2, 3, 4, 5, ...}: conjunto dos números inteiros e não-negativos. Note que Z + = N.

Z * + = {1, 2, 3, 4, 5, ...}: conjunto dos arquivos inteiros positivos e sem o zero.

Z - = {..., –5, –4, –3, –2, –1, 0}: conjunto dos números inteiros não-positivos.

Z * - = {..., –5, –4, –3, –2, –1}: conjunto dos tipos inteiros negativos e sem o zero.


Conjunto dos Números Racionais (Q)
O conjunto dos índices é representado por Q. Reúne todos os números que podem ser escritos na forma p / q, sendo p e q números inteiros e q ≠ 0.

Q = {0, ± 1, ± 1/2, ± 1/3, ..., ± 2, ± 2/3, ± 2/5, ..., ± 3, ± 3/2, ± 3 / 4, ...}


Nota que em todo o presente é racional. Assim, Z é um subconjunto de Q.


Subcontas dos Números Racionais
Q * = subconjunto dos números racionais não-nulos, liderados por números de 
racionais sem o zero.

Q + = é compatível com o zero.

Q = + subconjunto dos dados racionais positivos, com os números racionais positivos, sem o zero.

Q - = o remendo é errado, o que é encontrado é igual a zero.


Q * - = subconjunto dos números de dados negativas, antigas referências negativas, sem o zero.


Conjunto dos Números Irracionais (I)
O conjunto dos números irracionais é representado por I. Reúne os números decimais não exatos com uma representação infinita e não periódica, por exemplo: 3,141592 ... ou 1,203040 ...


Importante ressaltar que as dívidas periódicas são números racionais e não irracionais. Elas são números decimais que se repetem após a vírgula, por exemplo: 1,3333333 ...


Conjunto dos Números Reais (R)
O conjunto dos reais é representado por. Assim, temos que R = Q □ I. Além disso, N, Z, Q e eu são subconjuntos de R.

Mas, observe que é um número real, racional, ele não pode ser também irracional. Da mesma forma, se ele é irracional, não é racional.

Subconjuntos dos Números Reais

R * = {x ∈ R≠x ≠ 0}: conjunto dos números reais não-nulos.

R + = {x ∈ R x ≥ 0}: conjunto dos reais não negativos.

R * + = {x ∈ R│x> 0}: entre dos números reais positivos.

R - = {x ∈ R x ≤ 0}: conjunto dos números reais não positivos.


R * - = {x ∈ R│x }: conjunto dos números reais negativos.

PIRÂMIDE

A pirâmide é uma figura geométrica espacial, mais precisamente um poliedro.

Ela é composta por uma base e um vértice. Sua base pode ser triangular, pentagonal, quadrada, retangular, paralelogramo.

Já o vértice, corresponde ao ponto mais distante da base da pirâmide e que une todas as faces laterais triangulares.

Em outros termos, a pirâmide é um sólido geométrico de base poligonal que possui todos os vértices num plano (plano da base). Sua altura corresponde a distância entre o vértice e sua base.

Observe que o número de lados do polígono da base corresponde o número de faces laterais da pirâmide.

Elementos da Pirâmide

•  Base: corresponde à região plana poligonal na qual se sustenta a pirâmide.
• Altura: designa a distância do vértice da pirâmide ao plano da base.
• Arestas: são classificadas em arestas da base, ou seja, todos os lados do polígono da base, e arestas laterais, segmentos formados pela distância do vértice da pirâmide até sua base.
• Apótemas: corresponde à altura de cada face lateral; são classificadas em apótema da base e apótema da pirâmide.
• Superfície Lateral: É a superfície poliédrica composta por todas as faces laterais da pirâmide.

Tipos de Pirâmide

Segundo as bases e o número arestas que formam as pirâmides, elas são classificadas em:

• Pirâmide Triangular: sua base é um triângulo, composta de quatro faces: três faces laterais e a face da base:

• Pirâmide Quadrangular: sua base é um quadrado, composta de cinco faces: quatro faces laterais e a face da base.

• Pirâmide Pentagonal: sua base é um pentágono, composta de seis faces: cinco faces laterais e a face da base.

• Pirâmide Hexagonal: sua base é um hexágono, composta de sete faces: seis faces laterais e face da base.

No tocante à inclinação da base, as pirâmides são classificadas de duas maneiras:

• Pirâmides Retas, que formam um ângulo de 90º;

• Pirâmides Oblíquas, que apresentam ângulos diferentes de 90º.

Área da Pirâmide

Para calcular a área total da pirâmide, utiliza-se a seguinte fórmula:

Área total: Al + Ab

Onde,

Al: Área lateral (soma das áreas de todas as faces laterais)

Ab: Área da base

Volume da Pirâmide

Para calcular o volume da pirâmide, tem-se a expressão:

V=1/3 Ab.h

Onde:

Ab: Área da base

h: altura

FRAÇÕES

Na matemática, as frações correspondem a uma representação das partes de um todo. Ela determina a divisão de partes iguais sendo que cada parte é uma fração do inteiro.

Como exemplo podemos pensar numa pizza dividida em 8 partes iguais, sendo que cada fatia corresponde a 1/8 (um oitavo) de seu total. Se eu como 3 fatias, posso dizer que comi 3/8 (três oitavos) da pizza.

Importante lembrar que nas frações, o termo superior é chamado de numerador enquanto o termo inferior é chamado de denominador.

Tipos de Frações
Fração Própria
São frações em que o numerador é menor que o denominador, ou seja, representa um número menor que um inteiro. Ex: 2/7

Fração Imprópria
São frações em que o numerador é maior, ou seja, representa um número maior que o inteiro. Ex: 5/3

Fração Aparente
São frações em que o numerador é múltiplo ao denominador, ou seja, representa um número inteiro escrito em forma de fração. Ex: 6/3= 2

Fração Mista
É constituída por uma parte inteira e uma fracionária representada por números mistos. Ex: 1 2/6. (um inteiro e dois sextos)

Obs: Há outros tipos de frações, são elas: equivalente, irredutível, unitária, egípcia, decimal, composta, contínua, algébrica.


Operações com Frações
Adição
Nas adições fracionárias, utiliza-se o Mínimo Múltiplo Comum (MMC) realizado a partir de seus denominadores, ou seja, o menor número múltiplo dos dois.

Subtração

Tanto na adição quanto na subtração é necessário encontrar o Mínimo Múltiplo Comum, (MMC), isto é, os números múltiplos comuns aos denominadores.

Multiplicação
Na multiplicação fracionária, multiplicam-se os numeradores entre si, bem como seus denominadores.

Divisão

Na divisão entre duas frações, multiplica-se a primeira fração pelo inverso da segunda, ou seja, inverte-se o numerador e o denominador da segunda fração.

História das Frações

A história das frações remonta o Antigo Egito (3.000 a.C.) e traduz a necessidade e a importância para o ser humano acerca dos números fracionários.

Naquele tempo, os matemáticos marcavam suas terras para delimitá-las. Com isso, nas épocas chuvosas o rio passava do limite e inundava muitas terras e, consequentemente, as marcações.

Diante disso, os matemáticos resolveram demarcá-las com cordas a fim de resolver o problema inicial das enchentes.

Contudo, notaram que muitos terrenos não eram compostos somente por números inteiros, havia os terrenos que mediam partes daquele total.

Foi a partir disso, que os geômetras dos faraós do Egito, começaram a utilizar os números fracionários. Note que a palavra Fração é proveniente do latim fractus e significa “partido”.